느좋 인공지능
[ML Specialization / Andrew Ng] W1 Introduction to Machine Learning 본문
[ML Specialization / Andrew Ng] W1 Introduction to Machine Learning
serenewave 2025. 1. 14. 23:221) Overview of ML
ML: field of study that gives computers the ability to learn without being explicitly programmed.
즉 학습, 경험을 통해 수행하는 성능을 높여나갈 수 있는 기술을 머신러닝이라 한다.
머신러닝의 주요 알고리즘으로는
1 지도학습(Supervised learning): ML로 얻는 경제적 가치의 99%는 지도학습에 의한 것이다
2 비지도학습(Unsupervised learning)
+ 강화학습, 추천시스템..
2) Supervised vs Unsupervised ML
1 지도학습: 특정 input에 대한 output(right answer)의 데이터 셋 샘플이 주어져 둘의 관계(mapping)을 유추 하도록 하는 것이다. 쉽게말해 입력 데이터 $x$와 정답 label $y$를 알려주고 학습시키는 것이며, 새로운 $x'$을 주었을때 이에대한 $y'$을 예측하도록 하는것이 목표이다.
1-1 회귀(Regression): 연속적인 값(number)을 예측한다. 무한히 많이 가능한 output이 존재한다.
ex) 집 크기(x) -> 집 가격(y)에 대한 데이터 세트를 주고, 관계를 학습시켜 x'에 대한 y'를 예측시킨다.

1-2 분류(Classification): 클래스 레이블(cateogry)를 예측한다. 적은 수의 가능한 output이 존재한다.
ex) 종양 크기(0~100)에 따른 암 발병 여부(O,X)를 주고, 관계를 학습시켜 x'(종양크기)에 대한 y'(O,X)를 예측시킨다.
예측변수(x)도 1개가 아니라 여러개일 수 있고, 카테고리(y)도 2개(이진분류)가 아니라 여러개일 수 있다.

2 비지도학습: 정답이 없이 데이터(x) 만으로 학습한다. 데이터의 구조와 패턴을 이해하는 것이 목적이다(finding something interesting) 입력에 대한 정확한 답을 구하는 것이 목적이 아니므로 unsupervised이다.
ex) 단순히 데이터의 패턴을 파악한 후, 데이터를 두개로 그룹화할 수 있겠는데? -> clustering
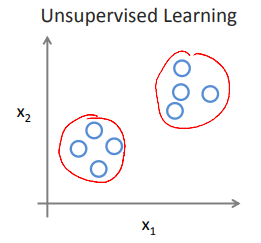
2-1 군집화(clustering): 같은 검색어 기준으로 기사를 그룹화 해서 띄우는 구글 뉴스 등에서 쓰인다.
2-2 이상탐지(Anomaly detection): find unusual data points
2-3 차원축소(Dimensionality reduction): compress data using fewer number
<아래는 공부하다 든 의문들>
Q1 머신러닝과 딥러닝을 어떻게 구분해야하나
A: 머신러닝 내부에 딥러닝이 있다. 그러나 지도/비지도/강화/딥러닝 이런 분류는 부적절하다. 딥러닝은 머신러닝의 여러 알고리즘 중에 여러 특징을 가진 알고리즘으로 지도, 비지도, 강화학습을 모두 이용할 수 있는 특별한 도구이다. 머신러닝 내부에 회귀, 분류, clustering, svd, ... , 딥러닝 등의 알고리즘(기법, 도구)가 있다! 로 이해하는 것이 낫다.
Q2 ML의 목적은 모두 답출력! 예측!인줄 알았는데, 비지도학습은 구조파악+패턴파악이 끝이라고 하니까 헷갈린다. 지도학습은 output을 내뱉으며 한 과정이 종결되는 느낌인데 비지도학습은 something interesting을 output으로 내뱉을 뿐으로 궁극적인 목적이 끝나지 않은 느낌이 든다.
A: '예측'은 지도학습에서나 의미있는 개념이며, 결과물이 예측값이라 목적이 바로 해결된다. 그러나 비지도학습은 데이터를 분석한 뒤의 구조가 결과물이므로, 이 자체가 큰 목적은 아니며 '다른 분석에 이용될 중간 결과물이다' 즉, 비지도학습의 결과물을 지도학습에 활용하는 경우가 많으며, 자체로 의미없는 것은 아니나, 예측/분류 같은 목표를 위해서는 지도학습에 결합해야 더 큰 효과를 본다. 예를들어, clustering을 이용하여 군집화 한 것이 의미가 없는 것은 아니나 이를 이용하여 지도학습을 통해 '분류'를 거쳐야 더 큰 효과가 생기는 것이다.
<break>
3) Linear regression model

training set라고 불리는 (x,y) 데이터가 주어지면 아래와 같은 그래프에 데이터에 맞는 모델(직선)을 그어서 집 크기에 대한 가격을 예측할 수 있다.
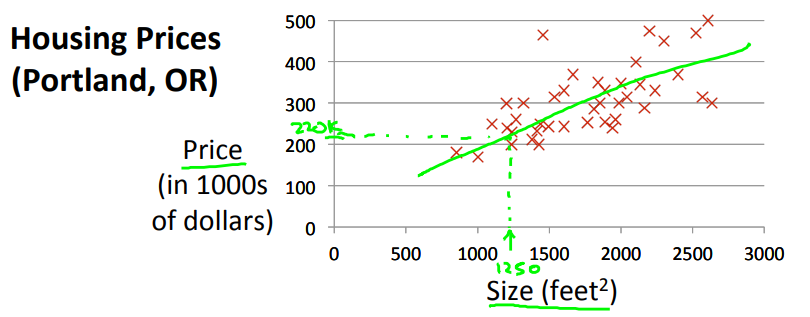
이렇듯 직선 모델을 구현한 뒤, 새로운 X'(1250)에 대한 Y'(220K)를 예측하므로 이는 지도학습, 그중에서도 회귀문제 라고 할 수 있다.
이 과정을 정리하자면, 주어진 Training Set를 이용하여 Learning Algorithm을 통해 적절한 모델(가설함수, h)를 도출한다. 이후, 이 모델에 새로운 값 x'에 대한 결과값 y'를 구하기 위해 함수 h에 x'를 대입하여 $y' = h(x')$ 의 과정을 통해 예측값을 구해낼 수 있게 된다.
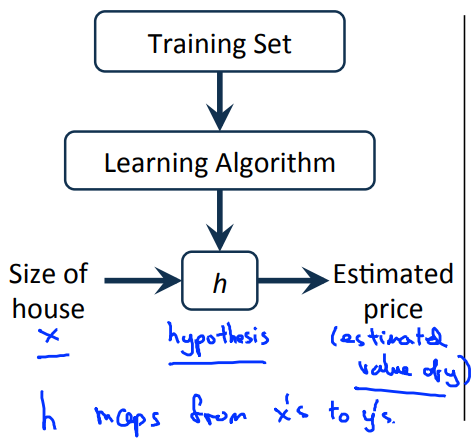
그렇다면, 어떤 모델이 가장 좋은 모델일까? 우리는 어떤 과정을 거쳐 이 h(x)에 해당하는 모델을 도출해낼 수 있을까?
(우선 단순 선형 회귀(1차함수: $h(x) = ax + b$)에 대해서만 고려한다. linear regression with one variable, univariate linear regression)
-> 비용 함수(Cost function)이라는 개념이 나온다.
비용 함수를 이용해, 적절한 파라미터 값(a, b)를 구하여 '가장 좋은 모델'을 구현해 내게 된다.
** $\sum loss(손실함수) = cost(비용함수)$
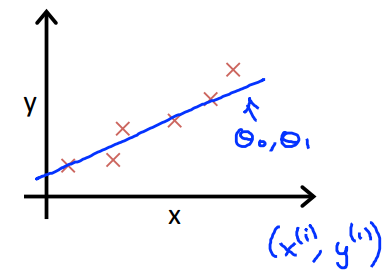
$Y = f(x) = wx + b$ 라고 할때, 점들을 가장 잘 표현하는 $(w,b)$를 찾는 문제는 모든 $(x,y)$에 대해서 가장 가까운 $Y$ 직선을 찾는 문제와 동일하다.
$error = \hat{Y} - Y$라고 할 때, $\sum_{}^{}(f(x)-y)^{2}$을 이용하여 비용함수는 아래와 같이 계산한다.
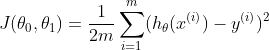
$2m$으로 나눠준 것은 계산의 편리함을 위한 것이며, 이는 평균제곱오차(Mean Square Error)로 볼 수도 있다.
그렇다면 위의 문제는 이제, 손실함수가 최소화 되도록 하는 $(w,b)$를 찾는 문제와 동일해진다.
그렇다면 손실함수가 최소화 되는 지점은 어떻게 찾을까?
->이에 대한 답은 미분, 경사하강법(Gradient Descent)에 있다.
*그전에 손실함수가 대충 어떻게 생겼을지에 대한 부분을 다룬다.
단순 선형 회귀에서의 손실함수는 이차함수 형태이므로 항상 convex하며 최소값을 가진다. 라는 결론만 이해하고 넘어가도 된다.
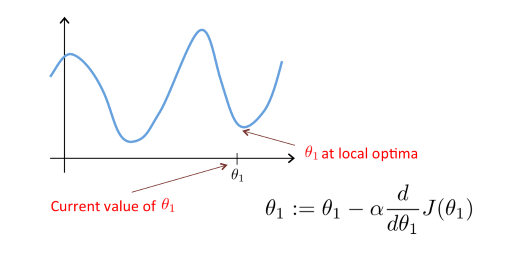
다른 모델에서의 손실함수는 이차함수보다 더 복잡한 형태일 것이며, 그에 맞게 여러 극소, 극대 지점을 갖는 그림으로 표현할 수 있다. 어떠한 그림이든, 경사하강법을 이용하여 local minimum에 도달하고 그 지점에서의 $(w,b)$를 최적의 $w$, $b$로 이해하고 잡으면 된다. (최적의 (w,b) = 'J가 최소' = $error^{2}$이 최소인 지점) -> 최적의 parameter value)

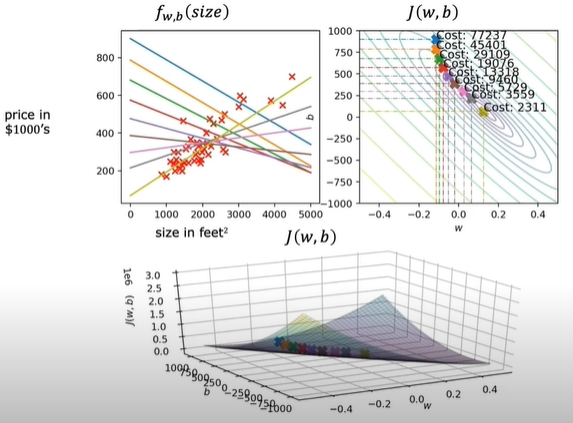
단순 선형 회귀에서의 손실함수 3차원 표현
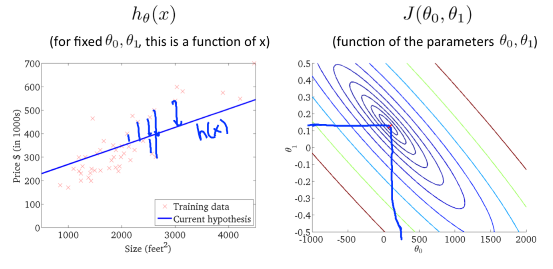
오른쪽은 손실함수를 등고선으로 표현한 것이다. 이때, 최소지점이 되는 $(\theta_{0} ,\theta_{1} )$를 찾는 것이 목표이다.
4) 경사하강법(Gradient Descent)
경사하강법은 비용함수(cost function)의 최소값을 구하는 알고리즘으로, 대부분 머신러닝에서 사용한다.
Gradient Descent 알고리즘은 다음과 같은 방법으로 진행된다.
1. Start with some $\theta_{0} ,\theta_{1}$
2. Keep changeing $\theta_{0} ,\theta_{1}$ to reduce $J(\theta_{0} ,\theta_{1})$ until we hopefully end up at a minimum
즉, 임의의 초기값으로 시작하여, 최소의 Cost Function 값을 찾을 때까지 $\theta_{0} ,\theta_{1}$을 변경시킨다. 임의의 초기값을 기준으로 최소가 되는 점을 찾아나는 알고리즘이다.
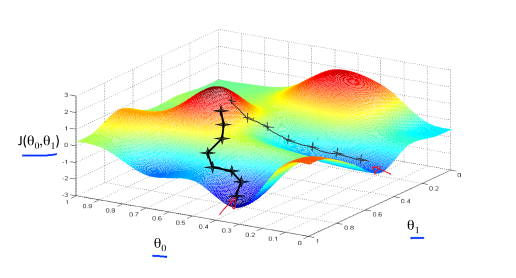
비용함수의 형태가 매우 다양하며 여러 local minimum이 존재할 수 있으므로, 초기값에 따라 도달하는 local minimum이 달라질 수 있다.
->그렇다면 $\theta_{0} ,\theta_{1}$ 를 어떤 값을 기준으로, 얼마나 reduce 해야하나?
어떤 값: 손실함수에대한 $\theta$의 미분계수
얼마나: 학습률(learning rate) $\eta$
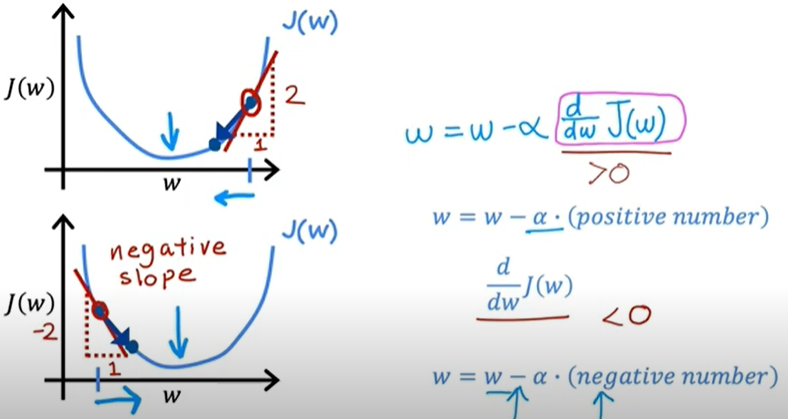
이를 수식으로 표현하면 다음과 같다.
$\theta_{j} := \theta_{j}-\eta \frac{\partial}{\partial \theta_{j}}J(\theta_{0}, \theta_{1})$
선형회귀에서는 파라메터 $\theta_{0}, \theta_{1}$가 $w, b$인 것으로 이해하면 된다.
코드로 표현할때, 아래 그림의 오른쪽처럼 표현하면, temp1의 값을 수정할때, 이전의 temp0이 아닌 수정된 temp0의 값으로 편미분을 진행한다는 오류가 있으므로 아래 그림의 왼쪽처럼 표현해야한다는 내용도 간단히 참고하면된다.

학습률이 너무 작다면 수렴하는데 너무 오래 걸리며, 너무 크다면 수렴하지 못하거나 발산한다. 그러므로 적절한 학습률 값을 설정하는 것이 중요하다.

또한, $\frac{\partial}{\partial w}J(w)$ 값 자체가 극점에 가까워지며 점점 줄어들기 때문에, 알아서 미분계수가 0인 지점에서 정지하게 되므로, 학습률 값은 상수이다.
그렇다면, 이제 이 경사하강법을 단순 선형회귀에 적용해보자.

cost function 식을 참고하여, $\frac{\partial}{\partial w} J(w,b)$ 와 $\frac{\partial}{\partial b} J(w,b)$를 구하면 아래와 같다.

이를 이용하여 단순 선형 회귀에서의 경사 하강법의 식을 아래와 같이 표현할 수 있다.

이렇게, $w$와 $b$를 계속 수정해 나간다는 것의 의미는, 계속 수정되는 $h(x)=wx+b$ 직선에 대하여 선형회귀를 여러번 적용하고, 수정되는 비용함수 값을 여러번 계산한다는 의미이다. 이 과정을 반복하다 경사하강법에서의 편미분값이 0이 되었을때 (=비용함수의 극소점에 도달했을때) 비로소 수렴된 최종적인 $w$, $b$값에 대한 '최적의 직선'을 구하여 이 직선으로 단순 선형회귀 방법을 적용하게 된다는 것이다. 이러한 말들을 그림으로 표현한 것이 아래이다.
참고로 선형회귀는 local minimum이 딱 하나 존재하여, 그 자체가 최소값이 되는 형태의 비용함수를 가지고 있으므로, 초기값이 크게 중요하지는 않다. (초기값이 도달하는 극점의 위치를 바꾸지는 않는다)
마지막으로, 'batch'라는 개념에 대해 배운다. 이는 모든 training set를 이용한다는 뜻이며, 경사하강법을 'batch gradient descent'로도 부른다. 점 하나가 데이터 하나일때, 모든 점을 다 이용하여 구한 비용함수를 기반으로 경사하강법을 이용하므로 배치작업이라 할 수 있다.
<정리>
1) ML의 기본 개념을 배우고
2) 지도/비지도 분류
3) 단순선형회귀. 최적 파라메터 값을 구하기 위해, 비용함수 개념을 배우고 비용함수가 최소가 되는 지점의 파라메터(w, b)를 구하여 단순선형회귀분석 식을 정하면 된다
4) 경사하강법. $\theta_{j} := \theta_{j}-\eta \frac{\partial}{\partial \theta_{j}}J(\theta_{0}, \theta_{1})$ 라는 경사하강법 식을 설명하고 이를 단순 선형회귀에 적용한 경사하강법 식을 보여주고 시뮬레이션까지 한다. + 배치 개념 설명
<코멘트>
회귀분석 과목을 배울때는 선형회귀 $h(x) = wx+b$에 대한 개념을 배우고, MSE를 배운 다음, MSE가 최소가 되는 w, b를 구해야한다. -> (계산을 이용하면) w와 b의 식은 ~다. 이러한 흐름으로 배웠다. 단순선형회귀에서는 미적분학/선형대수학 지식으로 'normal equation'을 이용하면 w와 b의 값을 바로 정할 수 있는 것이다. 그러나, 여기서는 두번째 방법으로 w, b 값을 최적의 값의 방향으로 점점 수정해나가는 경사하강법으로 w와 b를 구하는 과정을 설명한 뒤, normal equation에 대해서도 짧게 설명한다.
위 내용이 선형회귀 w, b 값 어떻게??->경사하강법 일반화설명-> 선형회귀에도 적용. 의 흐름인게 인상적이다.
'ML > 코세라 ML Specialization' 카테고리의 다른 글
| [ML Specialization / Andrew NG] W5 Neural Network training (0) | 2025.06.12 |
|---|---|
| [ML Specialization / Andrew Ng] W4 Neural Networks (0) | 2025.01.30 |
| [ML Specialization / Andrew Ng] W3 Classification (0) | 2025.01.18 |
| [ML Specialization / Andrew Ng] W2 Regression with multiple input variables (0) | 2025.01.18 |
| [ML Specialization / Andrew Ng / Coursera] (0) | 2025.01.14 |



